Linear Regression - Performance Checking & Diagnosis

Hello World, This is Saumya, and I am here to help you understand and implement Linear Regression in more detail and will discuss various problems we may encounter while training our model along with some techniques to solve those problems. There won't be any more programming done in this post, although, you can try it out yourself, whatever is discussed in this blog. 

So now, first of all, Let's recall what we studied about Linear Regression in our previous blog. So, we first discussed about certain notations regarding to machine learning in general, then the cost function, h_θ (x⁽ⁱ⁾)= θ₀ x₀+θ₁ x₁. Further we discussed about training the model using the training set by running the gradient descent algorithm over it. We also discussed about the Cost Function.

Now, before we begin, I want to talk about the Cost Function in brief. Cost function, as we defined, is, J(θ)= _i=1^m∑( h_θ(x⁽ⁱ⁾)-y⁽ⁱ⁾)²/ (2*m). If we define cost function, we can define it as the function, whose value is penalized by the difference between our expected value, and the actual value. Let's say, the value we obtain from h_θ (x⁽ⁱ⁾) is 1000, and the actual value should have been 980. So, we'll be adding a penalty to our model of 20². And so, the task at our hand while training the model is to actually tweak the parameters in such a way, that, this penalty is the least possible value, for all the data in training set.

We'll come back to this cost function later. Before that, let's see what a polynomial regression hypothesis looks like.

If we recall, for a linear regression, we define hypothesis as h_θ (x⁽ⁱ⁾)= θ₀ x₀+θ₁ x₁+θ₂x₂, for two variables x₀,x_1. For the sake of simplicity, let's assume, there is only one feature, let's say radius, of the ground x₀. Now, the cost will depend upon the diameter as well as area of the circle, for some crazy situation, let's assume. So, we can rewrite the hypothesis as h_θ(x⁽ⁱ⁾)= θ₀ x₀+θ₁ x₁+θ₂x₁².

So, our gradient term, that is derivative of the cost function, will become.

Ə J(θ)/ Əθ₁=  _i=1^m∑( h_θ(x⁽ⁱ⁾)-y⁽ⁱ⁾)² * x₁⁽ⁱ⁾/ m

Ə J(θ)/ Əθ₂=  _i=1^m∑( h_θ(x⁽ⁱ⁾)-y⁽ⁱ⁾)² * (x₁⁽ⁱ⁾)²/ m

So, in short, if we substitute x₁² with x₂, it wouldn't make any difference to our linear regression formulas. In sum, we can say, polynomial linear regression is basically multivariate linear regression, theoretically.

Now, we can use this to add new features to our training data, generate features as a combination of two features and so on, to improve accuracy of our model. But, does higher accuracy always help? Suppose a model has 98% accuracy on training data, but when deployed, performs poorly to real world scenarios. Simultaneously, suppose a model has 90% accuracy, but it can perform better than the previous model on the real world scenario.

What might cause this issue to occur?

Is it the training data or our model selection?

Let's see three different linear regression graphs.

As we can see, this graph, a straight linear h_θ(x⁽ⁱ⁾)= θ₀ x₀+θ₁ x₁, loosely fits the training sets, and we can say it is highly biased or partial to certain examples then the others. Such a type of model is called a under-fitted model or a model showing high bias. To remove this bias, and get rid of this problem of under fitting, we should try to add in extra features. So that our model can train and fit itself better. Increasing the size of our training data might not actually help us a lot in such a situation.

Let's say, to the above example, we added several features, so that our hypothesis becomes h_θ(x⁽ⁱ⁾) = θ₀ x₀+θ₁ x₁ + θ₂ x₁^1/2+ θ₃ x₁^1/3++ θ₄ x₁^3/2…. and so on… And so our model fits in this manner now.

As, we can observe, it shows a very high accuracy rate on our training data, but it tends to consider the noise in our training data to affect our models. Basically, it is trying to fit in some anomalous data into our training model as well. This gives rise to the problem of over fitting, or high variance, since, it lets the noise model our data. Reducing the features might help us in this case.

In short,          Under Fitting is low accuracy , high bias, low variance.

Whereas          Over Fitting is high accuracy, low bias, high variance.

Now, since we know the solution to over-fitting, how can we reduce the features in such a way that it doesn't stay over-fitted, but it doesn't fit either. Regularization comes into play now.

So, what is regularization?

If we recall earlier, we used to penalize the model with the difference in prediction for every training example. Let's say, while training our parameter's, we want the parameters to be so small, that the noise doesn't affect our model, but not too small that it under fits the training set. So, we'll add an extra term to our cost function. which is.

J(θ)= (_i=1^m∑( h_θ(x⁽ⁱ⁾)-y⁽ⁱ⁾)²/ (2*m)) + λ( _j=1ⁿ∑(θ²)/(2*m) )

Where, λ is called the regularization parameter. So, what are we actually doing. We are in fact, penalizing our model for ever parameter trained, so that our model will now try to reduce not only the prediction cost, but also the parameters accordingly, as possible.

Higher the value of λ, lesser will be the value of the parameters, and Vice Versa.

The question now is, what should be the degree of the polynomial and the value of λ for an ideal model that fits our training set appropriately. Let's answer these two questions one after another.

To find the ideal degree of our polynomial, we'll first divide our actual training set into two or three parts. The new training set, which would be 60% the size of our actual set, and the rest 40% would be divided either into Cross Validation Set and Testing Set or just Cross Validation Set. Now, we'll being with a single degree and increase the degree of our polynomial, and simultaneously, train and keep track of our Cost function value.

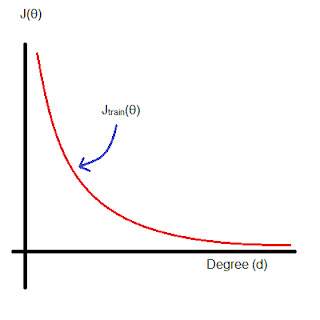
We'll notice something like this.

The graph will start with a very high value of cost/error function, for a very particular low degree of polynomial. But as we start increasing the degree of our polynomial function, note that the cost function starts decreasing. Note that this is done on the new training set and not on the actual training set.

Now, we'll take our cross-validation set and plot the same, cost v/s degree graph. It will turn out to be something similar to this.

So, for a low degree of polynomial, the cost will be high. And as it turns out, since the higher degree polynomial is intended to fit our training set data well, it will fit loosely to our cross-validation set. Note that, we are not supposed to train our machine using cross-validation data set. So what can we imply from this?

To summarize the above…

High Bias	High Variance
Low accuracy on Training Data	High accuracy on Training Data
Low accuracy on CV/Test Data	Low accuracy on CV/Test Data
J cv(θ) ≈ J train(θ)	J cv(θ) >> J train(θ)

 That gives us an idea on how to solve the degree of the polynomial problem. We are to find the value of the degree for which we get the lowest value of the cost function. Now, we'll move ahead towards the λ selection problem. what particular value of λ will give us an ideal model for our polynomial regression.

Let's look in detail at the λ term in the cost function, λ( _j=1ⁿ∑(θ²)/(2*m).

For our objective to minimize the cost function, if we pick a small value of cost function, suppose we choose a very small value of λ. Then, it implies that we're penalizing our cost function less for every value θ. It means that this term will be minimized slower since its value has less effect on our cost function and so our cost function will try to minimize the other term more. This results in less minimization of the parameters θ.

Similarly, if we pick a very high value of λ, what it means is that, even for small values of θ, we'll be penalizing our cost function with a  large value because of λ. To minimize the cost function J(θ), which is dependent on θ, the result will be in very small values of θ, which would in fact, in some cases, make the model linear and highly under fitting.

Let's plot the J _train(θ) à λ and J _cv(θ) à λ, so we can observe and summarize the results.

You must have understood already by watching at the curve.

For J _train(θ) à λ, Low value means over-fitting and as a result high accuracy.

And for J _cv(θ) à λ, We'll get high cost for very low value of λ, as well as for high value of λ.

To summarize the above…

Low λ	High λ
High accuracy on Training Data	Low accuracy on Training Data
Low accuracy on CV/Test Data	Low accuracy on CV/Test Data
J cv(θ) >> J train(θ)	J cv(θ) ≈ J train(θ)
High Variance	High Bias

So, first, we'll pick some values of λ, and train our model for each of them. Then,  we'll check them all for on our Cross-Validation set. Evaluate and Select the best model accordingly.

Sometimes, even the size of our data set can affect our model selection and optimization of our learning model. Does increasing the size of our training set or getting more data help us always? Does providing more training data to an incorrect model increase it's accuracy? Suppose, our learning algorithm is not performing well, and so either it is highly biased, or high in variance, and you immaturely decide collect more training data! How will that affect our training model? We'll take a deeper look into this problem for each of both the cases.

Let's begin with high bias. Suppose you don't know that it's highly biased. And you start feeding it more data, gradually increasing the size m of our training set, and meanwhile taking note of the cost function J _train(θ) and J _cv(θ) for every particular value of m. We have fixed our training model for now, i.e. decided the number of parameters to train on.

So, if small value of m, let's say 2 or 3, it will be easier to fit a linear line through it. But this will result in high error for some training example in our cross validation set. Now, if we increase the value of m, the cost error function increases as it becomes more difficult to fit the data to our hypothesis.  Meanwhile, if we train more and more data to our learning algorithm, the J _cv  is bound to decrease, as our learning algorithm has tried to fit in many of the training sets. But still, in the end, the error J _train(θ) and J _cv(θ) will be quite high, but almost similar to each other. Note that, plotting J(θ)àm is done to analyze the model and find out flaws, it can't be used to fix those flaws.

Let's assume that we have a high variance problem in our learning algorithm, but we don't know it, yet. So, we start doing the same thing, plotting the cost function against the size of m. We realize that as we increase the size of our training data set, as usual, the error for training set increases and the error of the cross validation set decreases.

J _train(θ)  increases with increase in m because it gets more difficult to fit a quadratic or polynomial equation on the training set. But when we reach the limit on the size of training data we have, we realize that there is a very big gap between the J _train(θ) and the J _cv(θ). If you had any more data, this size would have decreases even further. This implies that getting more data sometimes helps to solve high variance, as it might reduce the ratio of those noisy data points from our training set which our learning model tries to fit into.

It might all be confusing sometimes to understand and remember everything at once. So let's just summarize the blog using a practice problem.

Suppose, you have implemented regularized linear regression to predict the stock market prices. However, when you test your hypothesis on a new set of data, you find that it makes unacceptably large errors in its prediction. You have 6 choices in all.

1. Get more training examples.

2. Use smaller set of Features.

3. Get additional Features.

4. Get polynomial Features.

5. Decrease λ.

6. Increase λ.

So, first of all, you'll check for bias and variance.

Let’s say if you have high bias. Then it means that getting more training examples would increase the bias even further. Moreover, decreasing the set of features wouldn't fix the problem as well, as it will perform even loosely on the test data. However you can increase the set of features or create your own features from the given features by combination of exponent and multiplication. To solve high bias, you can decrease the value of λ for it as well.

Similarly, if you encounter high variance, you can try increasing the number of training example, so that the ratio of noisy data points decreases and our learning model can perform little better on test data. Decreasing the number of features to train your model with will help too, as not all features might be useful and you may be simply over fitting your model. Increase in λ also helps remove high variance.

In short.

Solution	Problem to Fix
Get more training examples.	To solve high variance problem.
Use smaller set of Features.	To solve high variance problem.
Get additional Features.	To solve high bias problem.
Get polynomial Features.	To solve high bias problem.
Decrease λ.	To solve high bias problem.
Increase λ.	To solve high variance problem.

That's it from this blog, if there are any suggestions, or corrections, feel free to mention in the comment section. Also if you have any doubts, feel free to ask.

References:-

- Machine Learning by Andrew Ng, Coursera.org (among the best MOOCs).